1. ゴトー日(5・10日)ってなに?
毎月5や10のつく日にはドル買い需要が増える──そんな市場の“アノマリー”を耳にしたことはありませんか?
今回は、この「ゴトー日はドル円が上昇しやすい」という通説を、過去の実データから検証してみます。
※ アノマリー → 株式市場などでの経験則。理論では説明できないが経験的には説明できる市場変動の法則。
仮説A:ゴトー日は日足でドル円が上昇しやすい?
トレーダーの間では、「ゴトー日(5や10のつく日)にはドル円が上昇しやすい」という見方がしばしば語られます。
その背景には、国内企業の決済タイミングやドル需要の偏りといった要因があるとされますが、それが実際にチャート上の動きとして表れているかどうかは、あまり深く検証されていないのが現状です。
今回は、過去数年分のドル円データを使って、このアノマリーに実際の裏付けがあるのかを確認してみました。
✅ 検証方法
- 対象通貨:USDJPY(ドル円)
- 時間軸:日足(D1)
- 期間 :2011年1月1日 ~ 2025年6月25日(約13.5年分)
- ゴトー日の定義:
- 毎月 5・10・15・20・25・30 日
- および月末最終営業日
- 分析指標:
- 各日の「終値 – 始値」(価格変化)
- 陽線率(上昇した日の割合)
- t検定による統計的有意性
📊 検証結果
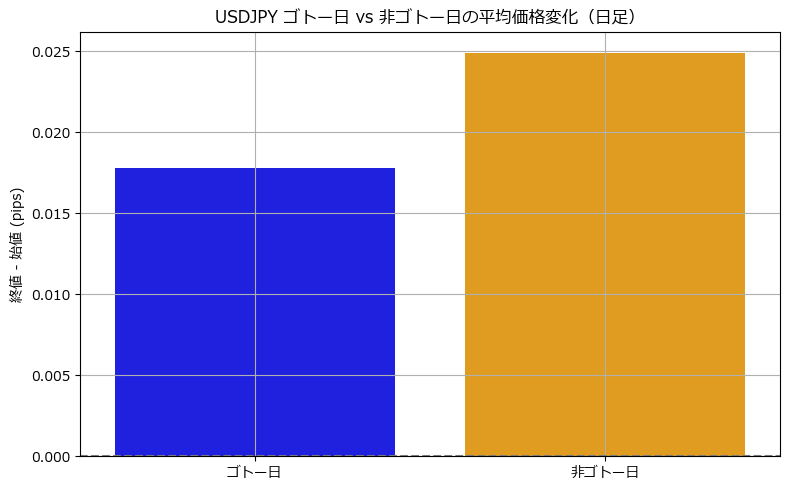
📈 分析指標
| 指標 | ゴトー日 | 非ゴトー日 |
|---|---|---|
| 平均価格変化(終値 – 始値) | +0.0178 | +0.0249 |
| 陽線率(上昇日比率) | 52.57% | 52.19% |
- ※価格変化は1営業日あたりの平均値(単位:円)
- 陽線率はその日の終値が始値を上回った割合
🔬 統計検定(t検定)
- ゴトー日と非ゴトー日の価格変化に有意な差があるかを検定
- 結果:p = 0.7959(p < 0.05 で有意とする)
🧪 p値が0.7959と高いため、「統計的に有意な差はない」と判断できます。
🧠 考察
この結果を見る限り、日足レベルでは「ゴトー日が有意に上昇しやすい」という根拠は確認できませんでした。
経験的には期待されていた「ドル買いによる上昇傾向」は存在するかもしれませんが、少なくとも今回のデータでは“偶然の範囲”と考えるのが妥当です。
🧪 次の検証へ
とはいえ、日足では“1日の中の変動”が埋もれてしまう可能性もあります。
そこで、次は「東京時間(9:00〜10:00)の1時間足」に絞った分析を行ってみます。
✅ 仮説B:ゴトー日の東京時間(9時台)は上昇しやすいのか?
「ゴトー日は東京時間に実需のドル買いが入りやすく、特に仲値(9:55)前の時間帯で上昇する」という見方があります。
この“時間帯アノマリー”は果たして事実なのでしょうか?
🔍 検証条件
- 対象通貨:USDJPY(ドル円)
- 時間軸:1時間足(H1)
- 分析対象:東京時間の9:00〜10:00
- 期間:2011年1月1日 ~ 2025年6月25日
- ゴトー日の定義:毎月5・10・15・20・25・30日、および月末
- 分析項目:1時間足の「close – open」(価格変化)
📈 結果:価格変化の統計比較(9時台)
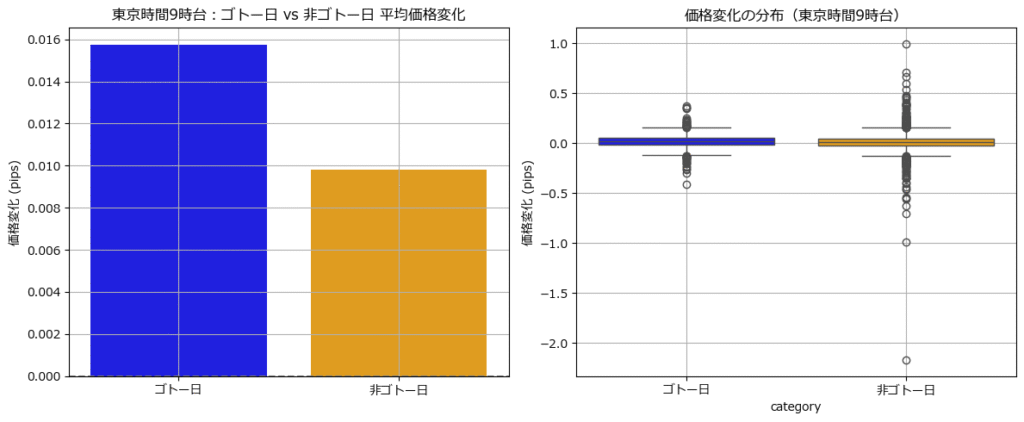
| 指標 | ゴトー日 | 非ゴトー日 |
|---|---|---|
| 平均 | +0.0158円 | +0.0098円 |
| 中央値 | +0.0150円 | +0.0080円 |
| 標準偏差 | 0.0740円 | 0.0988円 |
ゴトー日は非ゴトー日に比べて、平均的にやや上昇しやすい傾向が見られました。
🔬 t検定の結果(統計的有意性)
- p = 0.0615
この値は「有意水準5%(p < 0.05)」をやや上回っており、統計的に“有意”とは断言できないものの、“傾向は存在する可能性がある“と考えられます。
📈グラフ分析
🔹 左:平均価格変化(棒グラフ)
- ゴトー日の方が平均変動幅は大きく、価格は上昇方向
🔹 右:価格変化の分布(箱ひげ図)
- 両者とも外れ値が存在するが、ゴトー日の方が分布がやや狭く安定
- 非ゴトー日はボラティリティが高め
✅ 結論(仮説B)
🔍 「東京時間9時台に限定すれば、ゴトー日はやや上昇しやすい傾向が見られた」
他の要因(曜日・月末・為替介入前後)との関係性も検討余地あり
ただし、p値が0.0615のため、統計的に有意とは言えない点に注意が必要
次は曜日ごとの違いについて調べてみます。
✅ 仮説C:ゴトー日の効果は曜日によって異なるのか?
「ゴトー日でも金曜は逆行しやすい」「月曜は実需が少ない」など、FX市場では曜日ごとに“癖”があるのでは?と思いました。
なので、ゴトー日・非ゴトー日の価格変化を曜日別に集計し、ヒートマップで可視化して検証しました。
🔍 検証条件
- 対象通貨:USDJPY(ドル円)
- 時間軸:日足(D1)
- 検証期間:2011年1月1日~2025年6月25日
- 分析対象:各営業日の「終値 – 始値」
- ゴトー日の定義:毎月5・10・15・20・25・30日および月末
- 集計指標:曜日×カテゴリ(ゴトー日/非ゴトー日)の平均価格変化
📈 ヒートマップ結果
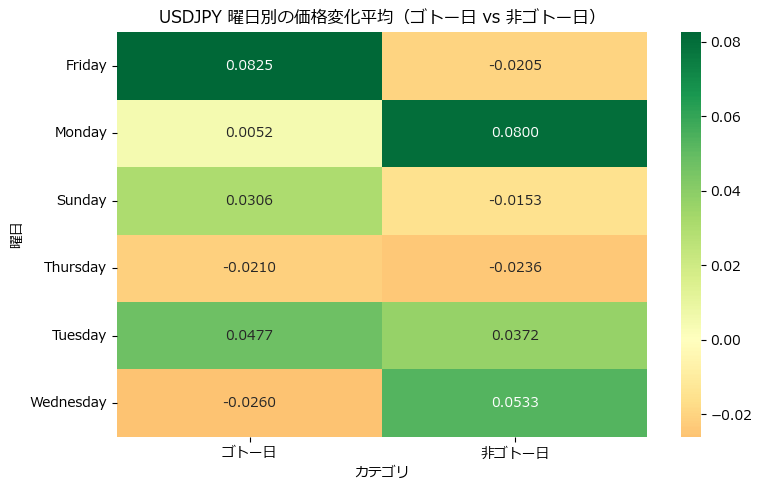
(図:曜日別 × ゴトー日分類による平均価格変化)
✅ 主な特徴:
| 曜日 | ゴトー日の傾向 | 非ゴトー日との比較 |
|---|---|---|
| 金曜 | +0.0825(高い) | 非ゴトー日は -0.0205 → 明確な差 |
| 水曜 | -0.0260(下落傾向) | 非ゴトー日は +0.0533 → 真逆の傾向 |
| 月曜 | わずか +0.0052 | 非ゴトー日は +0.0800 と大幅上昇 |
| 火曜・木曜 | 両カテゴリでそこまで差は小さい | 相関は弱め |
| 日曜 | 注:週明け早朝のスプレッドに注意(検証対象外も可) |
🔬 考察と示唆
- 金曜日は ゴトー日での上昇が特に顕著であり、非ゴトー日ではむしろ下落傾向という強い対照が見られました。
- 水曜日は 非ゴトー日で大きく上昇しやすく、ゴトー日で逆行傾向があるため、戦略的に注目度が高い曜日といえます。
- 曜日とゴトー日の複合的アノマリーがある可能性が高く、単に5日・10日だから買う、では不十分であることが分かります。
📝 結論(仮説C)
曜日別に見ると、ゴトー日の効果にはバラつきがあり、金曜や水曜は特に強弱が分かれやすいことが確認されました。
このように、「ゴトー日だから買う/売る」ではなく、「その日が何曜日か」も加味した上で、戦略を立てる必要があるといえるでしょう。
✅ ゴトー日アノマリー検証・結論まとめ
実戦活用には限定的な視点が重要
日足ベースでの大局的な信頼性は薄い一方、特定時間帯や曜日に絞れば、実戦戦略に取り入れる余地はある。
日足全体では有意差なし
2011年~2025年のUSDJPY日足データに基づく分析では、ゴトー日と非ゴトー日の「平均価格変化」「陽線率」に統計的有意差は確認されず。
東京時間9時台には注目すべき傾向
1時間足で東京9:00~10:00の動きに注目すると、ゴトー日の平均価格変化は非ゴトー日を上回っており、短期トレードには利用可能性あり。
曜日別では「金曜のゴトー日」が強い
曜日ごとの平均価格変化を可視化したところ、特に金曜日のゴトー日で上昇バイアスが顕著に見られた。
🔚 最後に
今回の分析から、ゴトー日には特定の時間帯や曜日においてわずかながらも特徴的な値動き傾向が見られることが確認されました。特に東京市場が本格的に動き出す9:00〜9:15前後や金曜日のゴトー日に注目することで、短期的な取引戦略に活用できる可能性があります。
ただし、本検証は過去の統計的傾向に基づいたものであり、未来の市場におけるパフォーマンスを保証するものではありません。相場は経済指標、地政学リスク、中央銀行の政策など多くの要因で変動するため、アノマリーに依存した取引には常にリスクが伴います。
あくまで参考材料の一つとして位置づけ、他のテクニカル・ファンダメンタル分析と組み合わせて慎重に判断することをおすすめします。
📘 おまけ:t検定とは何か?~ゴトー日検証の統計的裏付け~
🔍t検定の歴史:ギネスビールが生んだ統計手法?
t検定は、1908年にアイルランドの統計学者 ウィリアム・シーリー・ゴセット(William Sealy Gosset) によって考案されました。
彼は当時、アイルランドの有名なビール会社 ギネス社(Guinness) の研究者として働いており、
少ないサンプルからでも確かな品質判断を行う方法を必要としていました。
しかし、会社の方針で社員の研究成果は匿名で発表しなければならなかったため、
彼は「Student(スチューデント)」というペンネームで論文を投稿しました。
これが、今日でも使われている「Student’s t-test(スチューデントのt検定)」の語源です。
🍺 少ないデータでも信頼できる判断を――
この現実的なニーズから生まれたt検定は、今や経済学・心理学・医学・投資分野など幅広く応用されています。
∬t検定の目的
t検定は、2つのグループの平均に有意な差があるかどうかを調べる統計手法です。たとえば以下のような比較に使えます:
- ゴトー日 vs 非ゴトー日 の価格変化(例:終値 − 始値)
- 金曜日 vs 月曜日 の1時間足の変動幅 など
t検定の目的は、「その差が偶然のブレなのか、それとも明確な傾向として存在しているのか」を数字で判断することです。
📐 2. どうやって判断するのか?(p値の意味)
t検定を行うと「p値(p-value)」という結果が出てきます。この値は、「2つのグループの差が偶然に生じた可能性」を表します。
| p値 | 解釈 |
|---|---|
| p < 0.05 | 有意差あり(偶然ではない可能性が高い) |
| p ≥ 0.05 | 有意差なし(偶然のブレかもしれない) |
例えば、p = 0.03 であれば「統計的に意味のある差がある」と言えます。一方で、p = 0.40 なら「この差はたまたまでしょう」と判断します。
🧮 3. 実際の計算はどうなってるの?
Pythonなどを使えば自動でt検定が行えますが、仕組みとしては以下のような計算が行われています:
t = (平均1 – 平均2) / √(分散1 / n1 + 分散2 / n2)
- 平均1・平均2:各グループの平均値
- 分散1・分散2:標準偏差の2乗(データのばらつき)
- n1・n2:サンプル数(データの数)
この計算結果に応じて「p値」が出力されます。
🧠 4. 注意点と限界
- 正規分布が前提:価格変化の分布が大きく偏っている場合、t検定の前提が崩れることもあります。
- 平均値の差だけを見るので、分布の形や外れ値は考慮されません。
- サンプルサイズが小さいと、p値も不安定になりやすいです。
➡ だからこそ、t検定は「最終判断」ではなく「傾向の補足材料」として使うのが賢いです。
✅ まとめ
- t検定は、「平均値の差が偶然かどうか」を判定する統計手法
- p値が0.05未満なら「有意な差がある」とされる
- FX市場の検証において、主観ではなくデータに基づいた判断をするための有力なツール

コメント